ПАРАМЕТРИЧЕСКАЯ НАДЕЖНОСТЬ

Исключим из рассмотрения внезапные отказы. Тогда со­стояние системы, функционирующей в условиях случайных возму-. щений, можно полностью определить совокупностью п физических параметров Zj, Z2……………………….. Zn, принятых в качестве параметров состоя­

ния в силу их важности с точки зрения эффективности системы, выполнения его своего целевого назначения. Эти параметры можно

считать компонентами некоторого вектора Z в п-мерном фазовом пространстве состояний.

Исходя из назначения системы и физических принципов ее функ­ционирования, разделим фазовое пространство состояний некото­рой граничной поверхностью w (поверхностью предельных состоя­ний) на две области: область £2 работоспособных состояний и об­ласть отказов.

Параметрическая надежность есть вероятность того, что за вре­мя функционирования системы Т параметры состояния не выходят за допустимые пределы:

Рп == вер {ZQ 2} =

= вср [/?л /?12; /?21 ^2 ^ ’ ^?я1 <С-^л<С P-raJi ^ P)i

(L31)

где є — символ, указывающий на принадлежность вектора Z к области £2; Rn, R12, …, Дп2 — допустимые пределы, являющиеся ко­ординатами поверхности предельных состояний.

Если известна плотность распределения вектора Z, т. е. плот­ность f (zb z2, …, zJt^T) совместного распределения параметров — состояния в любой момент времени t, то параметрическая надеж­ность

Пересечение вектором Z в какой-либо момент времени по­верхности to предельных состояний означает выход системы из ра­ботоспособного состояния, т. е. отказ. В общем случае параметры состояния Zu Z2, …, Zn являются коррелированными случайными функциями времени и вычисление интеграла (1.32) сопряжено с

большими трудностями. Рассмот­рим возможные пути упрощения задачи.

Нередко можно пренебрегать изменением параметров состоя­ния во времени, т. е. считать па­раметры состояния случайными

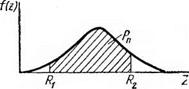
Рис. 1.3. Распределение параметра состояния, не зависящего от вре­мени

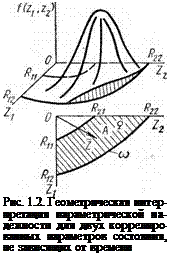
величинами. Такую постановку задачи назовем квазистатической. Для двух параметров состояния, не зависящих от времени, можно дать наглядную геометрическую интерпретацию параметрической надежности (рис. 1.2). Каждой паре значений параметров состоя­ния Z и z2 соответствует некоторая точка Л на плоскости ZiOZ2,

—►

определяющая модуль и направление вектора Z. Если точка А окажется вне области Q, то это означает отказ. Параметрическая надежность численно равна объему фигуры, ограниченной поверх­ностью f {z, z2) плотности совместного распределения параметров Z) и Z2 и плоскостью ZiOZ2 в пределах области Q:

^п = ВЄР {^?11 <С Н2 Z2 /?22і =

= Jj f{z 1, z^dzxdz2. (1.33)

Ri

Еще более просто интерпретируется один параметр состояния, не зависящий от времени (рис. 1.3): параметрическая надежность определяется площадью под кривой плотности распределения пара­метра состояния в установленных пределах:

«і

Вычисление интеграла (1.32) в квазистатической постановке не представляет особых трудностей, хотя объем расчетов суще­ственно растет с увеличением числа параметров состояния. Обычно для большинства систем ЛА удается ограничиться одним, реже двумя-тремя параметрами состояния. Так, для двигателя можно принять в качестве параметра состояния тягу, для топливной систе­мы— давление жидкости на входе в насос двигателя и т. п. В кон­кретных случаях не обязательно двустороннее ограничение пара­метра состояния, он может быть ограничен по физическим сообра­жениям только сверху или только снизу. Например, давление на входе в насос жидкостного реактивного двигателя должно быть не ниже требуемого по условию бескавитационной работы насоса, а угловая скорость вращения космического аппарата, отделяемого от ракеты-носителя,— не выше допустимой из условия его после­дующей стабилизации. ^

Законы распределения параметров состояния могут быть раз­личными, но часто полагают, что параметр состояния имеет нор­мальное распределение:

/ (г) = Д — — exp j —'{z ~ — I, (1-35)

У‘2паг I Н

где тг — математическое ожидание; oz2 — дисперсия.

Это дает возможность использовать для расчета вероятности Рп по одному параметру состояния табличную функцию (приложе­ние, табл. 3)

А’

ф(*)=—~ f е-‘зт. (1.36)

У~2п

При двустороннем ограничении параметра состояния парамет­рическая надежность (1.34)

Р.= Ф [(^2 — т,)1ах — ф 1(Я 1 — tnz)ioz. (1.37)

Если пределы симметричны относительно математического ожи­дания, т. е. 1^2— tnz = R—mz=R—tnz, то (1.37) преобразуется:

ЯП = 2Ф[(/? —mj/oj-l. (1.38)

При одностороннем ограничении параметра состояния в выра­жении (1.37) остается соответственно только один из членов. В этом случае удобно ввести новую переменную:

U—R — Z. (1.39)

В случае отличия закона распределения параметра состояния от нормального следует выполнять интегрирование плотности рас­пределения f(z) в соответствии с определением (1.34) каким-либо из известных методов (выражения плотности распределения для не­которых законов приведены в приложении, табл. 1). Наряду с этим

можно приближенно вычислить параметрическую надежность, ис­пользуя разложение Шарлье {36]:

оо

Рп— вер (U > 0} = j / (и) du Ф (т„/зи) —

О

~ Sh^imJou) + -~Ey (mjau), (1.40)

где U — параметр, определяемый выражением (1.39); Sk и Ех — соответственно асимметрия и эксцесс распределения; <р" и <р’" — табулированные вторая и третья производные плотности нормаль­ного распределения [8].

Есть и другие приближенные методы, основанные на аппрокси­мации плотности распределения f(u) рядом Эджворта или рядом Лаггера [55].

В общей квазистатической постановке при допущении нормаль­ного распределения параметров состояния определение параметри­ческой надежности сводится к вычислению /1-кратного интеграла вида (1.32) от плотности совместного нормального распределения л коррелированных случайных величин. В последнее время разра­ботан ряд методов решения этой задачи, основанных на пониже­нии порядка интеграла, аппроксимации его различными функция­ми, разложении в ряд по коэффициентам корреляции (например [32]), а также на использовании таблиц многомерных (до п=8) нормальных распределений [43]. В частности, для случая двух пара­метров состояния Uі и U2 параметрическая надежность

оо оо

Рп=вер {^>0, £/2>0}= Г Г/(иь Iia)d«1rfns=-i-®(a1)-f

0 0 2

+-f Ф(а2)-:г(аі, Pi)-Па* Pa), (1.41)

где a1 = m1/o1; a2=m2/o2; p!=(a2 — axrn) / (a^l — r?2); —

— a2ri2) / (a2^ 1 — ті2); mlt m2, Oj, a2, r12 —соответственно матема­тические ожидания, средние квадратические отклонения и коэффи­циент корреляции случайных величин Uі и U2 Т(а, Р) —табличная функция двумерного нормального распределения [43]. При отсут­ствии корреляции между параметрами Ux и U2

Яп=вер их > 0} вер [£/2 > 0} = Ф (0і) Ф (а2). (1.42)

При высокой надежности даже значительная корреляция оказы­вает слабое влияние на вероятность Рп, что является основанием для использования зависимостей вида (1.42).

Покажем на примере двух параметров состояния еще один ме­тод вычисления вероятности Ри при наличии корреляции. Приведем

исходное двухмерное нормальное распределение вектора Z к кано — 24

ническому виду (к некоррелированным составляющим) путем пре­образования координат [1]:

я>1=(«і — mZt) cos у — f (z2 — m2a) sin у; a>2= — Од — m*J sin Y + (z2 — m*,) cos у,

где у—— arctg-/’1-2-1°2- • Здесь имеется в виду, что <з1>о2, г12>0

2 а — а|

угол у положителен и лежит в первой чатверти. Для других слу­чаев нетрудно получить аналогичные выражения угла у.

В результате такого преобразования плотность совместного распределения f(zi, z2) распадается на множители fi(u>) и /2(^2) и параметрическая надежность

Rl R2

ВеР Z < Z2</?2] = J J /(?i, Z2)dzldz2 =

*1 я»’

=вер{1Г1</?|}вер{1Г2</?2}= j f1i‘w1)dwl J f2(w2)dw2=

—00 —00

= Ф(/?І/о»х)Ф(/?5/0. (1-44)

где в соответствии с зависимостями (1.43):

R = {Ri — mZl) cosy + (/?2 —m*2) sin у;

/?2= — (/?! — mZl) siny + (/?2 — m*,)cosy;

оШі = іАц cos2y -f — a2 sin2 у — 2r12o1o2 sin у cos y;

°k;2 = °.l sin2 У+ 02 COS2 у — 2r1201O2 sin у COS у.

Для трех и более коррелированных параметров состояния та­кой метод в принципе приемлем, но трудоемкость приведения рас­пределения к каноническому виду существенно возрастает.

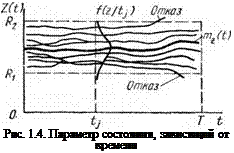
В ряде задач расчета параметрической надежности нельзя пре­небрегать изменением параметров состояния во времени. В этом случае методика расчета чаще всего основывается на теории вы­бросов случайных функций [49]. Геометрическая интерпретация за­дачи определения параметрической надежности как вероятности от­сутствия выбросов случайной функции Z(t) параметра состояния за уровни Ri и R2 в течение времени функционирования Т дана на рис. 1.4. Для наглядности показаны плотность распределения f{z/tj) реализаций функции Z(t) в фиксированном сечении t=tj и мате­матическое ожидание mz(t). Если в первом приближении полагать выбросы за уровни R и R2 независимыми случайными событиями, то вероятности их рассчитываются в отдельности.

Рассмотрим кратко основные положения теории выбросов при­менительно к дифференцируемому случайному процессу Z (t) изме­
нения параметра состояния, выбросы которого за фиксированный уровень R означают отказы. Ограничимся определением среднего числа и средней длительности положительных выбросов, под кото­рыми принято понимать пересечения уровня R реализацией функ­ции Z(t) снизу вверх (рис. 1.5) в отличие от пересечений сверху вниз, считающихся отрицательными.

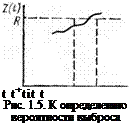Выброс в течение бесконечно малого интервала времени dt имеет место (рис. 1.5), если в начале интервала Z(t)<.R, а в конце Z(t) + V(t)dt>R, где В(/)>0 — скорость изменения функции Z(t).

Объединив неравенства, запишем вероятность выброса на интер­вале dt:

оо R

dQ=Bep{R-V(t)dt<Z{t)<R}= Г f f{z, v/t)dzdv,(lA5)

О R—Vdt

где f(z, v/t) —плотность совместного распределения ординаты Z(t) и скорости ее изменения V (t) в один и тот же момент времени.

Пределы внутреннего интеграла (1.45) отличаются на бесконеч­но малую величину; применяя теорему о среднем, имеем

ОО

dQ~dt j*/(R, v/ty’vdv. (1-46)

о

Таким образом, плотность вероятности положительного выбро­са функции Z(t) за уровень R в момент t

ОО

q (R/t)=dQ/dt=§f(R, Ф) vdv. (1.47)

о

Плотность вероятности отрицательного выброса выражается аналогичным интегралом, но в пределах от —оо до 0.

Чтобы найти среднее число выбросов за время Т, необходимо разделить промежуток Т на k интервалов длительностью dt, пола­гая, что более одного выброса на интервале из-за его малости не
может быть. Полное число выбросов за время Т есть дискретная случайная величина

N=^Nj, (1-48)

і-1

где Nj= 1, если на /-м интервале происходит выброс, в противном случае Nз = 0.

Математические ожидания случайных величин Nj численно рав­ны вероятностям выбросов на соответствующих интервалах, т. е. q(R/tj)dtj. Находя математическое ожидание суммы (1.48) в преде­ле при k-^oo, с учетом выражения (1-47) получаем, что среднее число выбросов за время Т

N=J f / (/?, v/t) vdvdt. (1.49)

0 0 «.

Среднее число выбросов в единицу времени

n=N/T. (1.50)

Для нестационарного случайного процесса n=n(t)—перемен­ное во времени (мгновенное) значение среднего числа выбросов в единицу времени.

Определим среднюю длительность выбросов. Полагая, что из-за малости интервалов dt ордината z(tj) функции Z(t) на /-м интер­вале может быть либо выше, либо ниже уровня R, введем в рас­смотрение случайные величины Lh равные dt, если z(tj) >R, и нулю в противном случае. Тогда общая продолжительность L нахожде­ния функции Z (/) выше уровня R составляет:

к

£ = 2 Lj. (1.51)

}=i

Математическое ожидание случайной величины Lj равно произ­ведению вероятности § f (z/tj) dz превышения уровня R ордина­той z(tj) на длину интервала dt. Исходя из этого и применив к ра­венству (1.51) теорему о математическом ожидании суммы, в пре­деле при k-^oo получаем выражение среднего времени пребывания функции Z(t) за уровнем R:

Тогда средняя длительность выброса

___ Г 03 /Г СО

l = L/N= ^f(z/t)dzdt f (7(/?> vftvdvdt. (1.53) м / о ‘k

Величина т, как и Я, в случае нестационарного случайного процесса на разных отрезках времени различна.

В инженерной практике часто имеют дело со стационарными случайными процессами, например при исследовании вибраций. Для стационарного случайного процесса параметры пит приобре­тают смысл средних характеристик, плотности распределения f(z/t) и f(R, vft) утрачивают зависимость от t, интегрирование по времени сводится к умножению на Т и, следовательно, среднее чис­ло выбросов в единицу времени

оо

Л = |/(Я. *»)Vdv, (1.54)

о

а средняя длительность выброса

оо I оо

t = f{z)dz / |/(/?, v)vdv. (1.55)

Нахождение закона распределения f(z) реализаций случайного процесса создает определенные трудности. На практике обычно по­лагают распределение f(z) нормальным. Установлено (49], что ор­дината Z(t) стационарного случайного процесса и скорость V(t) ее изменения в момент времени t — некоррелированные (а при нормальном распределении — независимые) случайные величины. Поэтому

f{z, «) = /(*)/.(*)=[і/ (°У2л)} e“(z-m2)1/2^ X

X [l / {У 2я)] (1.56)

где 4 — дисперсия скорости V.

Подставив выражение (1.56) в (1.54), находим

«=ІЛУ( 2яо,)] c-(R-m*y/2a*. (1.57)

Подставив затем в выражение (1.55) плотность нормального распределения f(z), определяемую первым сомножителем выраже­ния (1.56), а также найденное выражение п, получим

jj (і.58)

где Ф(лг) —табличная функция (1.36).

При статистической обработке реализаций стационарного слу­чайного процесса кроме математического ожидания mz определяет­ся корреляционная функция Kz{t) или спектральная плотность Sz(co). Корреляционная функция связана с дисперсией о22 соотно­шением

кг (t)=4p*(*),

где Pz(t)—нормированная корреляционная функция, характери­зующая стохастическую зависимость между взятыми на интервале х сечениями процесса Z(i). Дисперсия

al=Kz (0). (1.60)

Корреляционную функцию Kv(т) скорости V(t) как производной ординаты Z(t) находят двойным дифференцированием корреляци­онной функции процесса:

*’(т)=—£*•(*> • с-61)

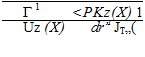Выразим отношение средних квадратических отклонений cv и cz через корреляционную функцию Kz(t) на основании (1.60) и (1.61): ____________ »

Гі-фЛ*—1ифШ=£1 L U’EeM 12^<о> і

(1.62)

Подкоренное выражение (1.62) можно сократить на az2 и, учиты­вая, что pz(0)s=l, получить

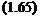А—і-]/ ~

2л V L dr 2 Jt=o

Па практике нормированную корреляционную функцию аппрок­симируют каким-либо выражением, например [49]:

Рг(т) = е_а|‘г|; p2(T)=e-°’,tlcos[iT;

рг(т)=е 1 cos^t;

Рг (Г) = Є—“ I т I ^COSpT + y Slnfi I t I j

где а, (3, аі, (Зі — параметры, определяемые по характерным точкам графика функции р2(т).

Параметр А можно выразить и через спектральную плотность Sz(co). Имея в виду, что

ОО

Кг (т) = f Sz (<о) cos ют^ш,

где to — круговая частота, получаем

Введем еще одно допущение, существенно облегчающее исполь­зование теории выбросов для расчета параметрической надежно­сти. При достаточно высокой надежности выбросы параметра со­стояния за установленный уровень можно считать редкими случай­ными событиями, подчиняющимися закону Пуассона. Поэтому параметрическую надежность как вероятность отсутствия выбросов в течение времени функционирования Т определяют в общем случае в соответствии с выражением (1.49) зависимостью

]•

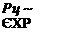
а для нормального стационарного случайного процессса — зависи­мостью

Л, « exp { — AT exp [ — (R — mJ/2Kz (0)]}, (1.70)

или

Рп^е~"Т. (1.71)

При наличии нескольких зависимых параметров состояния, представляющих собой случайные функции, задача существенно осложняется необходимостью введения в рассмотрение корреляци­онных функций связи.

Таким образом, для расчета параметрической надежности при известных законах распределения параметров состояния необходи­мо знать их числовые характеристики: в квазистатической поста­новке — математические ожидания, дисперсии и коэффициенты кор­реляции; при подходе к параметрам состояния как случайным про­цессам — математические ожидания и корреляционные функции (для стационарных процессов — спектральные плотности).